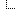Der Berührungspunkt ist (1|1)
Lösungsweg wäre der, dass 'a' deine Gerade genau an die Parabel legt, d.h. dass deine Gerade vom Nullpunkt aus um 'a' nach oben bzw. in diesem Fall nach unten verschoben werden muss.
EDIT: Ich habs, glaub ich:
Gleichsetzen war schon richtig. Wir wollen ja den gemeinsamen Schnittpunkt/Berührungspunkt von Gerade und Parabel.
Nun:
P = g
1/2x² + x - 1/2 = 2x + a
Folgt die quadratische Gleichung für x1,x2 = 1/2*(2 ± wurzel(4 + 4 + 8a))
Die Diskriminante muss nicht 1 sondern Null ergeben, damit es EINE Lösung gibt. Ist auch logisch, weil die vorgegebene Gerade nur einen Berührpunkt an die Parabel haben kann. Somit muss die Wurzel 0 werden, damit sie verschwindet.
8 + 8a = 0 folgt a = -1.
Hier kannst du jedenfalls Parabeln mit Geraden schneiden, und wennst für a = -1 einsetzt, dann - welch Zufall - bekommst die Lösung:
http://brinkmann-du.de/mathe/rbtest/1son...p_g_01.htm
vielleicht hat dir das ein bissl weitergeholfen.
Lösungsweg wäre der, dass 'a' deine Gerade genau an die Parabel legt, d.h. dass deine Gerade vom Nullpunkt aus um 'a' nach oben bzw. in diesem Fall nach unten verschoben werden muss.
EDIT: Ich habs, glaub ich:
Gleichsetzen war schon richtig. Wir wollen ja den gemeinsamen Schnittpunkt/Berührungspunkt von Gerade und Parabel.
Nun:
P = g
1/2x² + x - 1/2 = 2x + a
Folgt die quadratische Gleichung für x1,x2 = 1/2*(2 ± wurzel(4 + 4 + 8a))
Die Diskriminante muss nicht 1 sondern Null ergeben, damit es EINE Lösung gibt. Ist auch logisch, weil die vorgegebene Gerade nur einen Berührpunkt an die Parabel haben kann. Somit muss die Wurzel 0 werden, damit sie verschwindet.
8 + 8a = 0 folgt a = -1.
Hier kannst du jedenfalls Parabeln mit Geraden schneiden, und wennst für a = -1 einsetzt, dann - welch Zufall - bekommst die Lösung:
http://brinkmann-du.de/mathe/rbtest/1son...p_g_01.htm
vielleicht hat dir das ein bissl weitergeholfen.